二叉查找树(Binary Search Tree, BST)

• 1. 什么是二叉排序树？
• 2. 查找结点
• 3. 作业

1. 什么是二叉排序树？

二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。是数据结构中的一类。在一般情况下，查询效率比链表结构要高。

二叉排序树要么是空二叉树，要么具有如下特点（如图一就是一个二叉排序树）：

1. 二叉排序树中，如果其根结点有左子树，那么左子树上所有结点的值都小于根结点的值；
2. 二叉排序树中，如果其根结点有右子树，那么右子树上所有结点的值都大小根结点的值；
3. 二叉排序树的左右子树也要求都是二叉排序树；

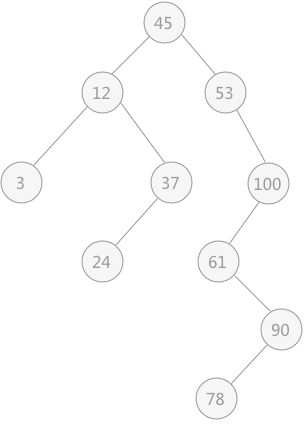图1 二叉查找树

2. 查找结点

It’s a very simple operation to perform.

Find(int n):

1. start from the root and compare root.data with n
2. if root.data is greater than n that means we need to go to the left of the root.
3. if root.data is smaller than n that means we need to go to the right of the root.
4. if any point of time root.data is equal to the n then we have found the node, return true.
5. if we reach to the leaves (end of the tree) return false, we didn’t find the element 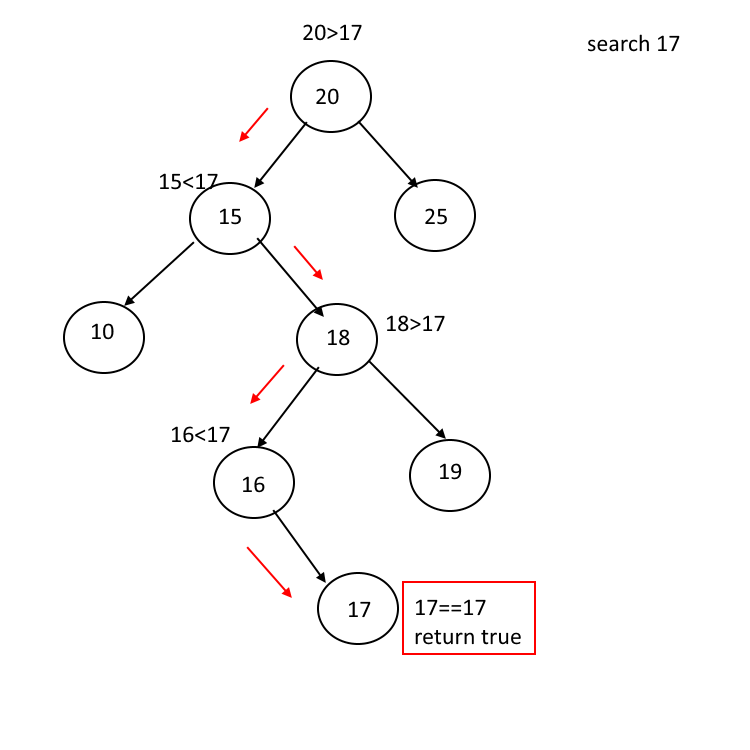图2 二叉查找树用于高效地查找数据

3. 作业

1、

【NOIP 2013 普及组初赛 q28】完善程序：
（二叉查找树） 二叉查找树具有如下性质： 每个节点的值都大于其左子树上所有节点的 值、小于其右子树上所有节点的值。试判断一棵树是否为二叉查找树。
输入的第一行包含一个整数 n，表示这棵树有 n 个顶点， 编号分别为 1, 2, ⋯ , n，其 中编号为 1 的为根结点。之后的第 i 行有三个数 value, left_child , right_child ，分别表示该节点关键字的值、左子节点的编号、右子节点的编号；如果不存在左子节点或右子节点，则用 0 代替。输出 1 表示这棵树是二叉查找树，输出0 则表示不是。

#include <iostream> 
using namespace std; 
const int SIZE = 100;
const int INFINITE = 1000000;
struct node
{
	int left_child, right_child, value;
}; node a[SIZE];
int is_bst( int root, int lower_bound, int upper_bound )
{
	int cur;
	if ( root == 0 )
		return(1);
	cur = a[root].value;
	if ( (cur > lower_bound) && ( ① ) && (is_bst( a[root].left_child, lower_bound, cur ) == 1) && (is_bst( ②, ③, ④ ) == 1) )
		return(1);
	return(0);
}


int main()
{
	int i, n; cin >> n;
	for ( i = 1; i <= n; i++ )
		cin >> a[i].value >> a[i].left_child >> a[i].right_child;
	cout << is_bst( ⑤, -INFINITE, INFINITE ) << endl;
	return(0);
}