二叉树（binary tree）是指树中结点的度不大于2的有序树，它是一种最简单且最重要的树。

1. 二叉树的性质

性质一：在二叉树的第i层上至多有2i−12^{i-1}个结点(i>=1)

证明：利用数学归纳法进行证明

当i==1时，第1层结点数目为 2i−1=21−1=20=12^{i-1} = 2^{1-1} = 2^0 = 1。显然成立，此时二叉树只有根结点。

假设i>1时，第i层的结点数目为2i−12^{i-1}，根据假设，只需证明第i+1层结点数为 2i2^i 即可。

由于二叉树每个结点最多有两个孩子，故第(i+1)层上的结点数最多是第i层的两倍。即：第i+1层上结点数最多为: 2×2(i−1)=2i2 \times 2^(i-1) = 2 ^ i

故假设成立，命题得证。

性质二：深度为k的二叉树至多有2k−12^k-1个结点

证明：二叉树结点数最多时，每层的结点树都必须最多。

根据性质一，深度为k的二叉树的结点数最多为: 20+21+....+2k−1=2k−12^0 + 2^1 +....+2^{k-1} = 2 ^ k -1

性质三： 具有n个结点的完全二叉树的高度为至少为log2(n+1)

证明：高度为h的二叉树最多有 2h–12^h – 1 个结点。反之，对于包含n个结点的二叉树的高度至少为 log⁡2(n+1)\log_{2}{(n+1)}。

性质四：对任何一棵二叉树T，n0=n2+1n_0 = n_2 +1。其中n0n_0是终端结点数目（度为0），n1n_1是度为1的结点数目，n2n_2是度为2的结点数目。

证明：二叉树结点度数最大为2，则结点总数目nn为：

n=n0+n1+n2n = n_0 + n_1 + n_2 （等式一）

从孩子个数角度出发： 度为0的结点没有孩子， 度为1的结点有1个孩子，度为2的结点有2个孩子，孩子总数为： Children=n0×0+n1×1+2×n2=n1+2×n2Children = n_0 \times 0 + n_1 \times 1 + 2 \times n2 = n_1 + 2 \times n2。

树的所有结点中，只有根不是任何结点的孩 子，因此有 n=Children+1n = Children + 1 ,即

n=n1+2∗n2+1n = n_1 + 2 * n_2 + 1 （等式二）

由等式一、等式二而可以推出 n0=n2+1n_0 = n_2 +1

2. 满二叉树

除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。

国内教程定义：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树。

3. 完全二叉树

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

性质五：如果对一棵有n个结点的完全二叉树的结点按层序编号（从第一层开始到最下一层，每一层从左到右编号），对任一结点i有：

如果i=1 ，则结点为根结点，没有双亲。

如果2 * i > n ，则结点i没有左孩子 ；否则其左孩子结点为2*i . （n为结点总数）

如果2 * i+1>n ，则结点i没有右孩子；否则其右孩子结点为2*1+1

3.1 完全二叉树的数组表示法

参考:http://data.biancheng.net/view/193.html

二叉树的顺序存储，指的是使用顺序表（数组）存储二叉树。需要注意的是，顺序存储只适用于完全二叉树。换句话说，只有完全二叉树才可以使用顺序表存储。因此，如果我们想顺序存储普通二叉树，需要提前将普通二叉树转化为完全二叉树。

普通二叉树转完全二叉树的方法很简单，只需给二叉树额外添加一些结点，将其”拼凑”成完全二叉树即可。如图 1 所示：

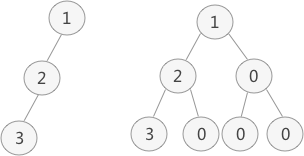
图 1 普通二叉树的转化

图 1 中，左侧是普通二叉树，右侧是转化后的完全（满）二叉树。

解决了二叉树的转化问题，接下来学习如何顺序存储完全（满）二叉树。

完全二叉树的顺序存储，仅需从根结点开始，按照层次依次将树中结点存储到数组即可。

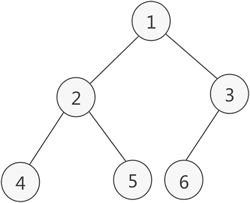
图 2 完全二叉树示意图

例如，存储图 2 所示的完全二叉树，其存储状态如图 3 所示：

图 3 完全二叉树存储状态示意图

同样，存储由普通二叉树转化来的完全二叉树也是如此。例如，图 1 中普通二叉树的数组存储状态如图 4 所示：

图 4 普通二叉树的存储状态

由此，我们就实现了完全二叉树的顺序存储。

不仅如此，从顺序表中还原完全二叉树也很简单。我们知道，完全二叉树具有这样的性质，将树中结点按照层次并从左到右依次标号（1,2,3,…），若结点 i 有左右孩子，则其左孩子结点为 2 * i，右孩子结点为 2 * i+1。此性质可用于还原数组中存储的完全二叉树，也就是实现由图 3 到图 2、由图 4 到图 1 的转变。

4. 代码示例

5. 编程

  1. noip-j-18-4 对称二叉树
  2. noip-j-04-3 FBI 树

6. 作业

1、

【CSP 2020 入门组第一轮 q12】独根树的高度为 1。具有 61 个结点的完全二叉树的高度为（ ）。
A. 7   B. 8   C. 5   D. 6  

2、

【CSP 2019 入门组第一轮 q08】一棵二叉树如右图所示，若采用顺序存储结构，即用一维数组元素存储该二叉树中的结点（根结点的下标为1,若某结点的下标为i ,则其左孩子位于下标2i处、右孩子位于下标2i+l处），则该数组的最大下标至少为（）。

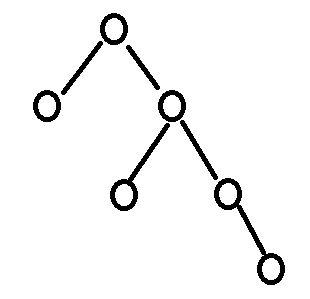
A. 6   B. 10   C. 15   D. 12  

3、

【NOIP 2018 普及组初赛 q07】根节点深度为 0，一棵深度为 h 的满 k（k>1）叉树，即除最后一层无任何子 节点外，每一层上的所有结点都有 k 个子结点的树，共有（ ）个结点。
A. (kh+1−1)/(k−1)(k^{h+1}-1)/(k-1)   B. kh−1k^{h-1}  
C. khk^h   D. (kh−1)/(k−1)(k^{h-1})/(k-1)  

4、

【NOIP 2016 普及组初赛 q11】一棵二叉树如右图所示，若采用顺序存储结构，即用一 维数组元素存储该二叉树中的结点（根结点的下标为 1， 若某结点的下标为 i ，则其左孩子位于下标 2i 处、右孩 子位于下标(2i+1)处），则图中所有结点的最大下标为（ ）。


A. 6   B. 10   C. 12   D. 15  

5、

【NOIP 2016 普及组初赛 q22】约定二叉树的根节点高度为 1。一棵结点数为 2016 的二叉树最少有（）个叶子结点；一棵结点数为 2016 的二叉树最小的高度值是（ ）。

6、

【NOIP 2015 普及组初赛 q17】如果根的高度为 1,具有 61 个结点的完全二叉树的高度为( )。
A. 5   B. 6   C. 7   D. 8  

7、

【NOIP 2015 普及组初赛 q22】一棵结点数为 2015 的二叉树最多有___个叶子结点。

8、

【NOIP 2014 普及组初赛 q16】一棵具有5层的满二叉树中结点数为( )。
A. 31   B. 32   C. 33   D. 16  

9、

【NOIP 2013 普及组初赛 q09】已知一棵二叉树有10 个节点，则其中至多有（ ）个节点有 2 个子节点。
A. 4   B. 5   C. 6   D. 7  

10、

【NOIP 2011 普及组初赛 q07】如果根结点的深度记为1，则一棵恰有2011个叶结点的二叉树的深度最少是（ ）。
A. 10   B. 11   C. 12   D. 13  

11、

【NOIP 2010 普及组初赛 q05】如果树根算第1层，那么一棵n层的二叉树最多有（ ）个结点。
A. 2n−12^{n}-1   B. 2n2^{n}  
C. 2n+12^{n}+1   D. 2n+12^{n+1}  

12、

【NOIP 2010 普及组初赛 q19】完全二叉树的顺序存储方案，是指将完全二叉树的结点从上至下、从左至右依次存放到一个顺序结构的数组中。假定根结点存放在数组的1号位置，则第k号结点的父结点如果存在的话，应当存放在数组的（ ）号位置。
A. 2k   B. 2k+1  
C. k/2下取整   D. (k+1)/2下取整  

13、

【NOIP 2009 普及组初赛 q14】一个包含nn个分支结点（非叶结点）的非空二叉树，它的叶结点数目最多为：
A. 2n+12n+1   B. 2n−12n-1   C. n−1n-1   D. n+1n+1  

14、

【NOIP 2008 普及组初赛 q18】设T是一棵有n个顶点的树，下列说法不正确的是（ ）。
A. T有n条边   B. T是连通的  
C. T是无环的   D. T有n-1条边  

15、

【NOIP 2008 普及组初赛 q05】完全二叉树共有2N−12N-1个结点，则它的叶节点数是（ ）。
A. N−1N-1   B. NN   C. 2N2N   D. 2N−12^N-1