树(Tree)
1. 数据结构的分类
我们先回顾一下数据结构的定义。数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。
“结构”就是指数据元素之间存在的关系,分为逻辑结构和存储结构。逻辑关系是指元素之间的前后间关系,与他们在计算机中的存储位置无关。
常见的逻辑结构如下:
- 集合:数据结构中的元素之间除了“同属一个集合” 的相互关系外,别无其他关系;
- 线性结构:数据结构中的元素存在一对一的相互关系。例如一维数组、栈、队列、链表。特征如下(以一维数组int arr[100]为例):
- 集合中必存在唯一的一个”第一个元素”;(例中的arr[0])
- 集合中必存在唯一的一个”最后的元素”;(例中的arr[99])
- 除最后元素之外,其它数据元素均有唯一的”后继”;(例中,arr[5]的后继元素为arr[6])
- 除第一元素之外,其它数据元素均有唯一的”前驱”(例中,arr[6]的前驱元素为arr[5])
- 树形结构:数据结构中的元素存在一对多的相互关系。例如二叉树。
- 图形结构:数据结构中的元素存在多对多的相互关系。
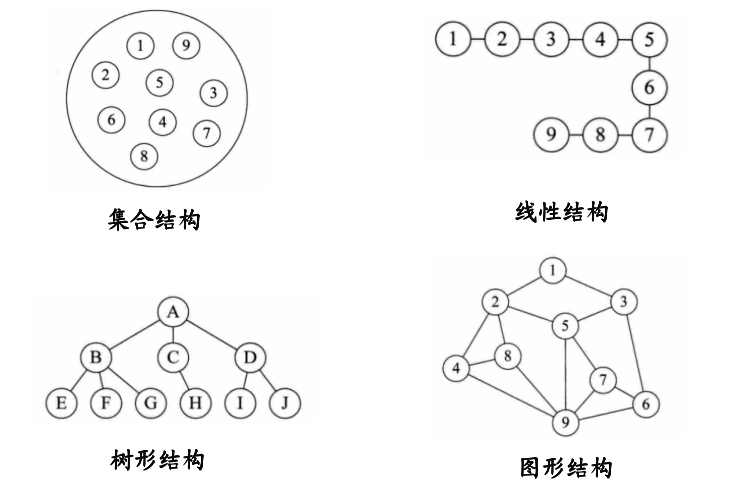
前面我们主要学习了线性结构,后面我们将继续学习树、图两种数据结构。
2. 树的基本概念
结点和度
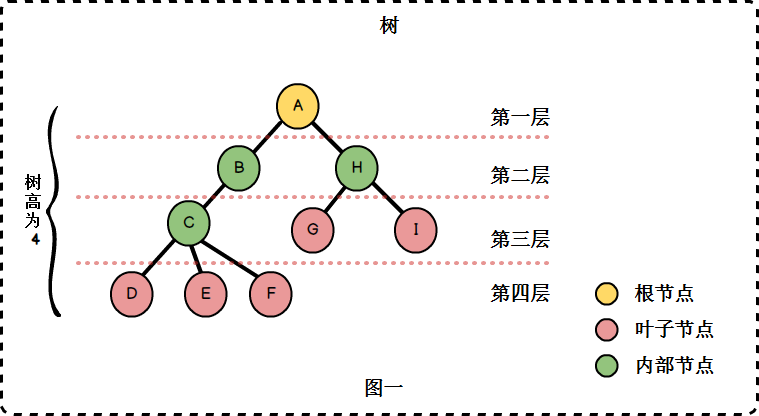
- 结点(Node):表示树中的数据元素,由数据项和数据元素之间的关系组成。在图中,共有9个结点。
- 根结点(Root):如图一中的A。
- 结点的度(Degree of Node):结点所拥有的子树的个数,在图中,结点A的度为2,结点C的度为3,结点D的度为0。
- 树的度(Degree of Tree):树中各结点度的最大值。在图中,树的度为3。
前后间的关系
- 子树:除了根结点外,每个子结点都可以分为多个不相交的子树。
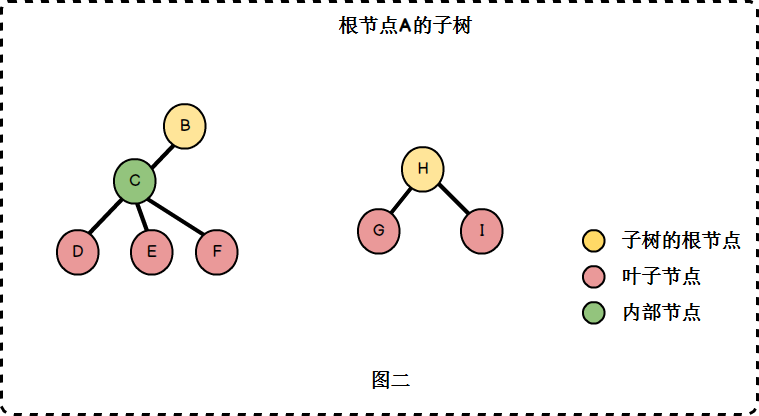
- 孩子(Chile)与双亲(Parent):若一个结点有子树,那么该结点称为子树根的”双亲”,子树的根是该结点的”孩子”。在图一中,B、H是A的孩子,A是B、H的双亲。
- 兄弟(Brother):具有相同双亲的结点互为兄弟,例如B与H互为兄弟。
结点的位置
- 叶子结点(Leaf Node):没有子树,也即是度为0的结点。如图一中的D、E、F、G、I。
- 分支结点(Branch Node):除了叶子结点之外的结点,也即是度不为0的结点。如图一中的A、B、C、H。
- 内部结点:除了根结点之外的分支结点。如图一中的B、C、H。
树的大小
- 层次:根结点为第一层(注意:根结点有时会被定义为第0层),其余结点的层次等于其双亲结点的层次加1。如图一中的C位于第3层。
- 树的高度:也称为树的深度,树中结点的最大层次。如图一中树的高度为4。
3 树的存储
参考网址:http://data.biancheng.net/view/196.html
3.1 双亲表示法
在树结构中,除了树根外,每个结点都只有一个父结点(又叫“双亲结点”)。
取一块连续的内存空间,在存储每个结点的同时,各自都附加一个记录其父结点位置的变量。
#define tree_size 100 //宏定义树中结点的最大数量
#define TElemType char //宏定义树结构中数据类型
struct NodeType{
TElemType data; //树中结点的数据类型
int parent; //结点的父结点在数组中的位置下标
};
struct TreeType {
NodeType nodes[tree_size]; //存放树中所有结点
int r; //根的位置下标
int n; //根的结点数
};
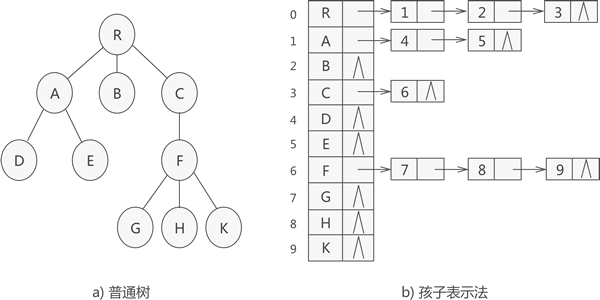
例如,使用双亲表示法存储图 1(A)中的树结构时,数组存储结果为(B):
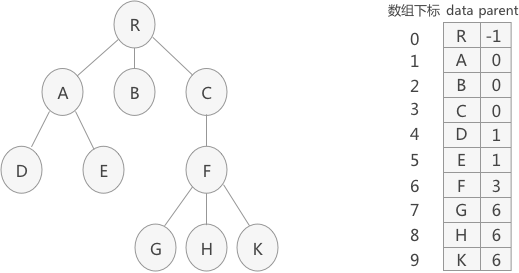
当算法中需要在树结构中频繁地查找某结点的父结点时,使用双亲表示法最合适。当频繁地访问结点的孩子结点时,双亲表示法就很麻烦,采用孩子表示法就很简单。
3.2 孩子表示法
将树中的每个结点的孩子结点排列成一个线性表,用链表存储起来。对于含有 n 个结点的树来说,就会有 n 个单链表,将 n 个单链表的头指针存储在一个线性表中,这样的表示方法就是孩子表示法。
如果结点没有孩子(例如叶子结点),那么它的单链表为空表。
#define TElemType char
#define tree_size 100
//孩子表示法
struct CTNode{
int child; //链表中每个结点存储的不是数据本身,而是数据在数组中存储的位置下标
struct CTNode * next;
};
struct NodeType {
TElemType data; //结点的数据类型
CTNode * firstchild; //孩子链表的头指针
};
struct TreeType{
NodeType nodes[tree_size]; //存储结点的数组
int r; //根的位置下标
int n; //根的结点数
};
例如,使用孩子表示法存储图 1 (A),存储效果如图 2: