数学和计算机的结合——牛顿法求一个数的平方根

1. 数学真题：求2的平方根的近似值

题目来源：2017 北京市朝阳区初一(下)期末，第26题

（1） 下面是小李探索 $\sqrt{2}$的近似值的过程，请补充完整:

我们知道面积是2的正方形的边长是$\sqrt{2}$，且 $\sqrt{2}>1$.设 $\sqrt{2}=1+x$，可画出如下示意图.

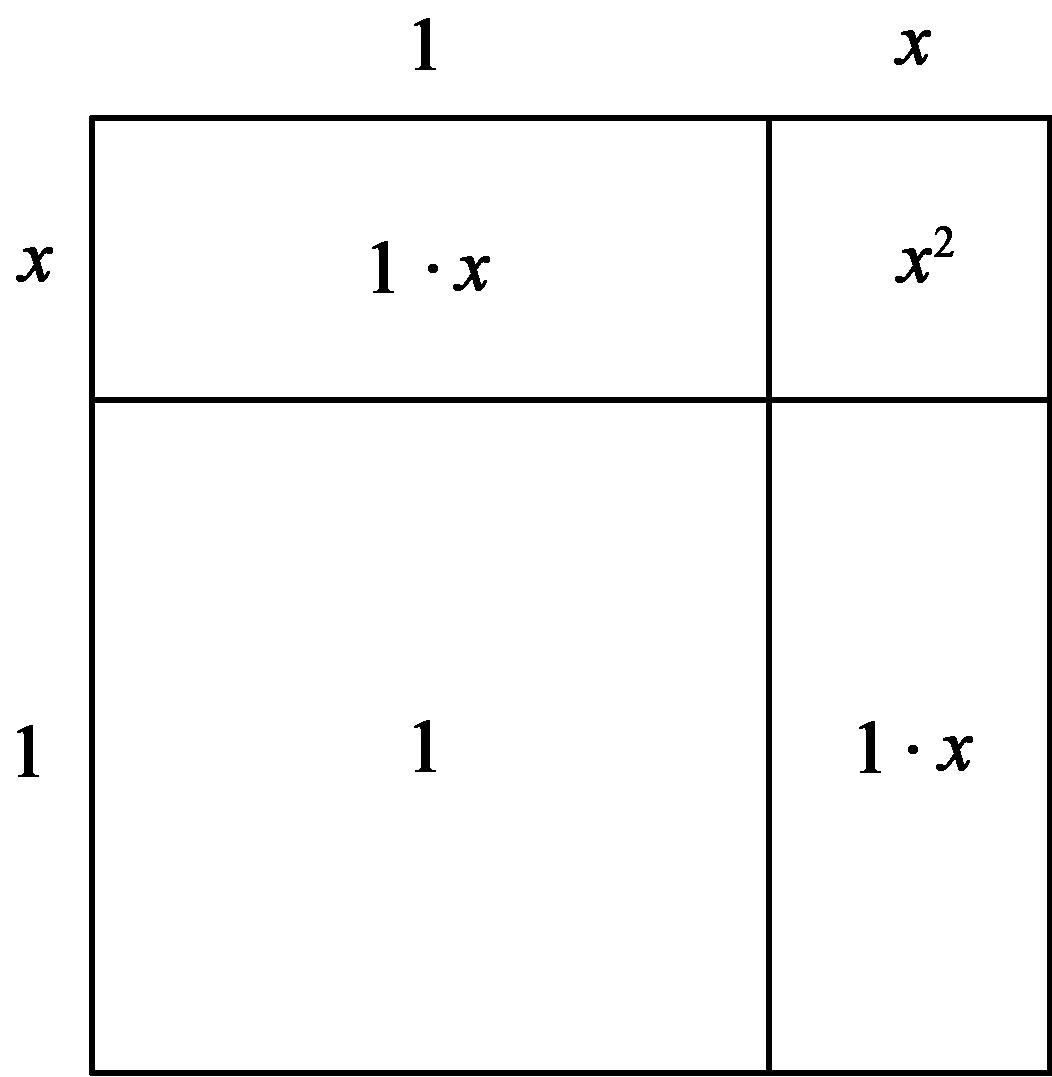
由面积公式，可得 $x^2 + \rule[-1pt]{3cm}{0.05em} =2$．

略去$x^2$，得方程 $\rule[-1pt]{3cm}{0.05em}$．

解得$x = \rule[-1pt]{3cm}{0.05em}$，即 $\sqrt{2} \approx \rule[-1pt]{3cm}{0.05em}$．

（2）仿照上述方法，利用（1）的结论，再探究一次，使求得的 $\sqrt{2}$ 的近似值更加准确．（画出示意图，标明数据， 并写出求解过程）

2. 数学探索

继续探索，求通用公式，找到类似牛顿法的公式。

3. 牛顿迭代法

3.1 牛顿迭代法简介

备注：需要用到切线、导数知识，初中生仅供粗略知晓

牛顿迭代法（Newton’s method）又称为牛顿-拉夫逊方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。牛顿迭代法是求方程根的重要方法之一。另外该方法广泛用于计算机编程中。

设$r$是$f(x) = 0$的根，选取$x_0$作为$r$初始近似值，过点$(x_0,f(x_0)$做曲线$y = f(x)$的切线$L$，$L$的方程为$y = f(x_0)+f'(x_0)(x-x_0)$，求出L与x轴交点的横坐标 $x1 = x_0-\frac{f(x_0)}{f'(x_0)}$，称$x_1$为$r$的一次近似值。

过点$x_1,f(x_1)$做曲线$y = f(x)$的切线，并求该切线与x轴交点的横坐标 $x_2 = x_1-\frac{f(x_1)}{f'(x_1)}$，称$x$2为$r$的二次近似值。重复以上过程，得r的近似值序列，其中

$$x_{n+1}=x_n－\frac{f(x_n)}{f'(x_n)}$$

称为$r$的$n+1$次近似值，上式称为牛顿迭代公式。

3.2 牛顿迭代法在求平方根中的应用

对于一个数字的根式，我们可以表示成 $x^2=p$，即$x^2-p=0$，对应的 $f(x)=x^2-p$。取导数得$f'(x)=2x$。

根据牛顿迭代的原理，可以得到以下的迭代公式：

$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)} = x_n-\frac{x^2-p}{2x} = \frac{x_n+\frac{p}{x_n}}{2}$$

3.3 求平方根的过程示例

求n的平方根，先随便取一个不是0的数作为迭代开始的$x_0$，例如最简单的$x_0=1$，然后反复代入$x_{k+1} = 0.5(x_k+\frac{n}{x_k})$求得下一个$x$，代入次数越多解约精确。

例如，以下仅保留7位小数为例，5的平方根（2.2360680）：
$x_0 = 1$
$x_1 = \frac{1 + \frac{5}{1}}{2} = 3$
$x_2 = \frac{3 + \frac{5}{3}}{2} = 2.3333333$
$x_3 = \frac{2.3333333 + \frac{5}{2.3333333}}{2} = 2.2380952$

就这样，反复代入上式计算，得到的值越来越精确。

3.4 计算机编程：求平方根（牛顿法）

求num的平方根的c++示例：

#include <iostream>
#include <iomanip>
using namespace std;
double sqr(double num)
{
   double k = 1.0;
   while (abs(k * k - num) > 1e-9)
   {
      k = (k + num / k) / 2;
   }
   return k;
}
int main()
{
   //2.2360680
   cout << setiosflags(ios::fixed) << setprecision(7) << sqr(5) << endl;
   return 0;
}

4. 计算机编程：求平方根（二分法）

#include <iostream>
#include <iomanip>
#include <cmath>
using namespace std;

double binary_search_sqrt(int num)
{
    double left = 0, right = num;
    double result = (left + right) / 2;
    double diff = result * result - num;
    while (abs(diff) > 1e-9)
    {
        if (diff > 0)
        {
            right = result;
        }
        else
        {
            left = result;
        }
        result = (left + right) / 2;
        diff = result * result - num;
    }
    return result;
}

int main()
{
    //num>1
    int n;
    cin >> n;
    cout << "binary_search:" << setiosflags(ios::fixed) << setprecision(12) << binary_search_sqrt(n) << endl;
    cout << "cmath        :" << setiosflags(ios::fixed) << setprecision(12) << sqrt(n) << endl;
}

思考：形式上看，在求根式这个特例上，牛顿法和二分法是不是很相像？都是取两个数的平均值，但是牛顿法对于第二个数的取法更加巧妙，用$p/x_n$来快速接近，同时不用考虑差异的符号。